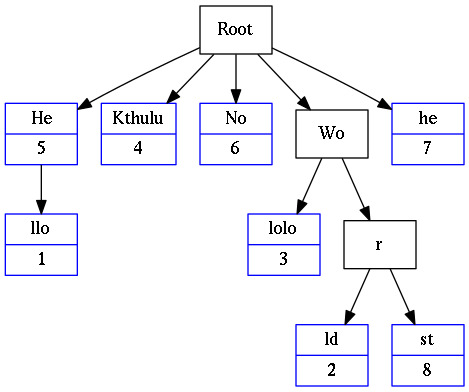
Trie, Ternary Search Tree (TST) and Radix Tree is aimed to compare the performance of these three data structures. The three data structure are an implementation of the abstract data type dictionary, but they are enhanced with an extra method called “keys”. That method returns the keys with that share a provided prefix. This can useful to use it in tasks such as autocomplete searches.
The study performed was using std::map and std::unordered_map as baseline for the performance.
Robert Sedgewick claims that a Ternary Search Tree (TST) is a better solution than a Radix Tree since it does not waste space if the amount of data is not dense enough. and Steven S. Skiena.
However, Steven S. Skiena holds that a Suffix Tree is the best approach, but since both data structures do not fulfill the same problems. I decided to use a Radix Tree regarding the close it gets to an Suffix Tree implementation.
Operations supported
The opeartions supported by Trie, Ternary Search Tree (TST) and Radix Tree are:
| Operations | Description |
|---|---|
| clear | Removes all the content of the data structure |
| find | Returns the value stored in the data structure for a specific key provided |
| insert | Adds a new pair of key and value to the data structure |
| size | Returns the amount of elements stored in the data structure |
| show | Prints the content of the data structure in the dot format |
| erase | Removes the value stored in the data structure for a specific key provided |
| contains | Returns true if there is a value associated to the key provided |
| keys | Returns a std::vector with all the keys in the data structure that have the provided prefix. If no prefix is provided returns a std::vector with all the keys in the data structure |
| lcp | Returns the longest common prefix of all keys stored in the data structure |
Scenarios tested
Several test scenarios have been have developed to compare the performance of these five data structures.
- Memory
- Random values
- Dictionaries
- Insert
- Random values
- Remove
- Random values
- Found
- Not found
- Dictionaries
- Found
- Not found
- Random values
- Seach
- Random values
- Found
- Not found
- Dictionaries
- Found
- Not found
- Random values
- Get Keys
- Random values
- Dictionaries
- Get Keys with Prefix
- Random values
- Dictionaries
- Longest Common Path
- Random values
- Dictionaries
Description of the structures
Trie
A trie is an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Values are not necessarily associated with every node. Rather, values tend only to be associated with leaves, and with some inner nodes that correspond to keys of interest.
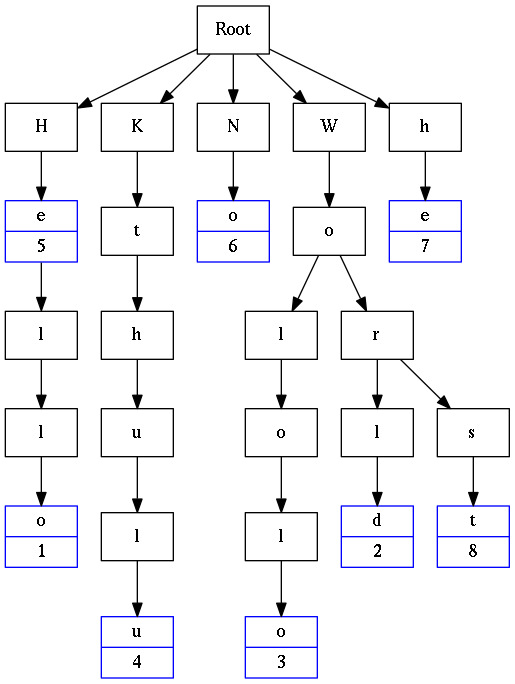
Ternary Search Tree (TST)
Ternary Search Tree is a type of trie (sometimes called a prefix tree) where nodes are arranged in a manner similar to a binary search tree, but with up to three children rather than the binary tree’s limit of two. Like other prefix trees, a ternary search tree can be used as an associative map structure with the ability for incremental string search. However, ternary search trees are more space efficient compared to standard prefix trees, at the cost of speed.
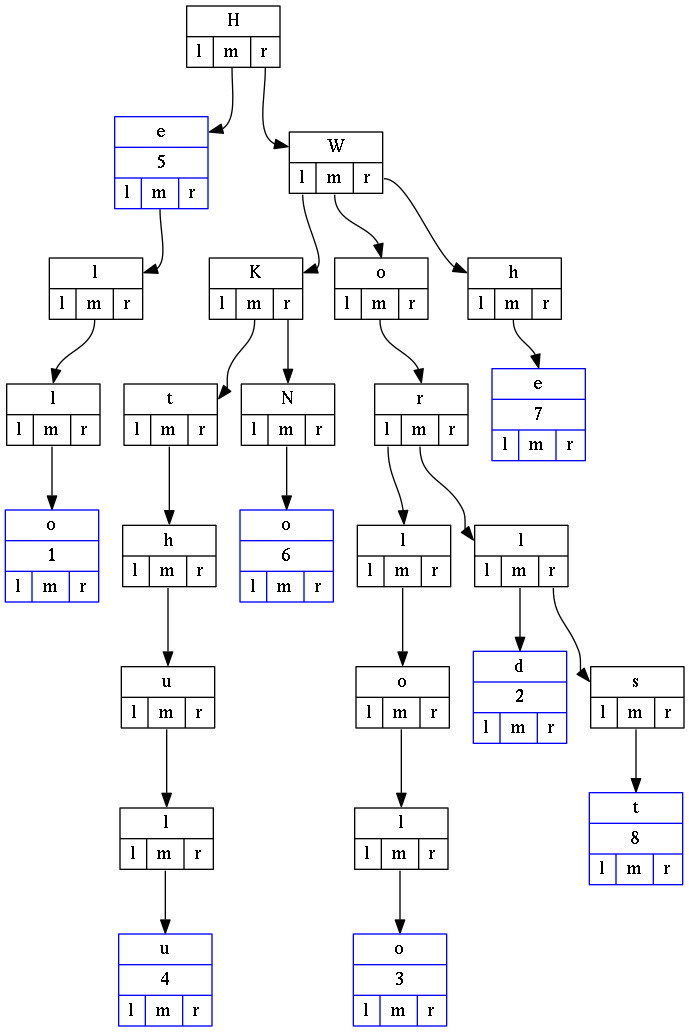
Radix Tree
Radix Tree (also radix trie or compact prefix tree) is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at least the radix r of the radix trie, where r is a positive integer and a power x of 2, having x >= 1. Unlike in regular tries, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets (especially if the strings are long) and for sets of strings that share long prefixes.
Results
All results can be seen here